Stellar Energy Losses

Key:

  1. Cooling speed of white dwarfs, and neutron stars
  2. “Delay of helium ignition in low mass red giants”[Raffelt]
  3. Helium burning lifetime

Evolution of Stars

Videos

Here is website that provides nice videos of evoution on HR digram, http://rainman.astro.illinois.edu/ddr/stellar/beginner.html

Main Sequence

  1. Formation: gas clound condense due to EM radiation.

    Negative Specific Heat

    Gravitation dominated systems usually have negative specific heat. As the volume contracts, the star would be heated up, since specific heat is defined as

    \[C = \frac{\delta Q}{dT}.\]

  2. Pressure, angular momentum, magnetic fields

  3. IMF: [0.08, 100] \(\mathscr M_\odot\)

    Salpeter’s IMF

    \[\frac{dN}{d\mathscr M} \propto ( \mathscr M/\mathscr M_{\odot} )^{-1.35}\]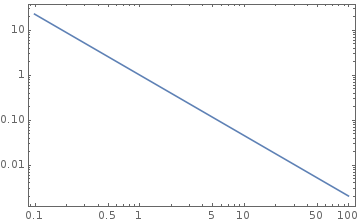
    ../_images/salpeter-imf.png

    Fig. 30 Salpeter’s IMF

    Notice that \(\int x^{-n} dx = C + \frac{ x^{1-n} }{1-n}\).

  4. First stars:

    1. mass fraction of hydrogen \(X\sim 0.75\)
    2. mass fraction of helium \(Y\sim 0.25\)

    Sun:

    metallicity: \(Z\sim 0.02\)

  5. Mass loss:

    1. stellar wind
    2. supernova explosions

  6. Limit of white dwarfs: 1.4 solar masses

  7. Disk of spiral galaxies: active death and birth of stars

    1. Spiral galaxies have old halo stars, globular clusters.

    2. Milky Way: 150 of them, each with \(10^{6}\) stars.

    3. Gravitational escape velocity of them: \(10\mathrm{km s^{-1}}\)

      Escape velocity

      From where?

    4. Supernova explosion ejects at \(10^{3}\mathrm{km s^{-1}}\).

    5. Supernova sweep whole globular cluster clean of gas.

      Ah?

      How?

    6. No star formation

    7. Good for stellar evolution research.

  8. Viral theorem, negative specific heat -> contraction -> nuclear burning

    1. determined by mass
    2. HR diagram: \(\log ( L/L_\odot )\) ~ \(\log ( T_{\mathrm{eff}}/K )\), or luminosity ~ surface temperature, scaled with solar quantities
    3. Most of the time the stars stay on the diagram
    4. Sun: 1Gyr life, half gone
    5. \(L\sim \mathscr M^3\)
    6. \(\mathscr M/\mathscr M_\odot \leq 0.7 - 0.8\) stars are still alive
    7. Globular cluster has turnoff: compare Fig. 2.2 and Fig. 2.3

  9. MS mass-radius relation: \(R \sim \mathscr M^\xi\), for \(\mathscr M < \mathscr M_\odot\), \(\xi \sim 0.8\), for \(\mathscr M > \mathscr M_\odot\), \(\xi \sim 0.57\); The difference comes from the convective envolope. [rbc3]

Red Giant

  1. Hydrogen consumed in center

  2. Next step depends on the mass of the stars

  3. For \(\mathscr M \leq 2 \mathscr M_\odot\)

    1. New configuration forms from helium ashes in the center

    2. Outer region expand -> Surface temperature drops -> Redder: red giant

      Why

      According to Stefan-Boltzman law?

      \[j = \sigma T^4\]

    3. There exists a hydrogen burning shell -> Dumps He into core

    4. He core is dense -> electrons degenerate -> mass-radius relation: \(R\sim \mathscr M^{-1/3}\) -> Mass of core increas leads to decrease in radius

    5. Core gravitation: \(\Phi_c \sim - G \mathscr M_c / R_c \sim \mathscr M^{4/3}\)

    6. Larger core mass -> Hotter hydrogen -> faster burning of hydrogen

References and Notes

[Raffelt]Stars as Laboratories for Fundamental Physics
[rbc3]http://personal.psu.edu/rbc3/A534/lec18.pdf