Special Functions

There are a lot of useful special function in physics. Some of them provides physics understanding of the problem, some of them helps us writing down a solution quickly.

Among them, Gamma functions, Legendre polynomials, Bessel functions, spherical harmonics, modified bessel functions, spherical bessel functions, and elliptical functions are the most used ones.

Gamma Functions

Gamma function satisfies the following relatioin,

\[\Gamma(z+1) = z\Gamma(z) .\]

For some cases, it can also be written as

\[\Gamma(n) = \int_0^\infty dt t^{n-1} e^{-t} .\]

One can prove that

\[\Gamma(z)\Gamma(1-z) = \frac{\pi}{\sin(\pi z)} .\]

Legendre Polynomials

Legendre polynomials are solutions to Legendre equation, which is

\[\left(\frac{d}{dx}\left[(1-x^2)\frac{d}{dx}\right] + n(n+1)\right) P_n(x) = 0.\]

Legendre polynomials has many different representations.

Integral

\[P_n(z) = \frac{1}{2\pi i} \oint (1 - 2 t z + t^2)^{1/2} t^{-n-1} dt.\]

Rodrigues representation

\[P_n(z) = \frac{1}{2^l l!} \frac{d^l}{d x^l} (x^2 - 1)^l .\]

It’s generation function is

\[\frac{1}{\sqrt{1 + \eta^2 - 2 \eta x }} = \sum_{k=0}^\infty \eta^k P_k(x) .\]

Properties

Orthogonality

\[\int_{-1}^1 P_m(x) P_n(x) dx = \frac{2}{2n + 1}\delta_{mn} .\]

They all have value 1 at \(z=1\).

The parity is alternating.

Examples

\[\begin{split}P_0(x) & = 1 \\ P_1(x) & = x \\ P_2(x) & = \frac{1}{2}(3x^2-1).\end{split}\]

Through these, we can solve out

\[\begin{split}x &= P_1(x) \\ x^2 &= \frac{1}{3}(P_0(x) + 2 P_2(x) ).\end{split}\]

Notice that they have physics meanings although it’s better to understand it together with spherical harmonics.

Associated Legendre Polynomials

The associated Legendre equation is

\[\left(\frac{d}{dx}\left[(1-x^2)\frac{d}{dx}\right] + n(n+1) - \frac{m^2}{1-x^2} \right) P_n(x) = 0.\]

The solution to this equation is Associated Legendre polynomial, which can be represented by

\[P_n^{\nu}(x) = (-1)^m(1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x) .\]

Bessel Functions

Bessel functions are solutions to Bessel equation,

\[\left( x \frac{d}{dx} x \frac{d}{dx} + x^2 - \nu^2 \right) J_{\nu} (x) = 0.\]

They all satisfy these recurrence relations,

\[\begin{split}Z_{n+1} + Z_{n-1} &= \frac{2n}{x} Z_n \\ Z_{n-1} - Z_{n+1} & = 2 \frac{d}{dx}Z_n .\end{split}\]

Bessel Function of the first kind

Use notation \(J_n(x)\) for the first kind.

Generating function is

\[e^{\frac{z}{2}\left(t-\frac{1}{t}\right)} = \sum_{n=-\infty}{infty} t^n J_n(z) .\]

Integral representation

\[J_n(z) = \frac{1}{2\pi} \int_{-\pi}^{\pi} e^{i(n\tau - x \sin \tau)} d\tau .\]

It also has a summation representation,

\[J_\alpha(z) = \sum_{m=0}^\infty \frac{(-1)^m}{m!\Gamma(m+\alpha +1)} \left( \frac{x}{2} \right)^{2m+\alpha} .\]

At large \(\vert x \vert\) limits, we have

\[\begin{split}\lim_{\vert x\vert \to \infty} J_l(x) &= \frac{\sin(z-l\frac{\pi}{2})}{x} \\ \lim_{\vert x\vert \to \infty} J_l'(x) &= \frac{\cos(z-l\frac{\pi}{2})}{x} .\end{split}\]

By playing with the recurrence relation,

\[\begin{split}2J_n' &= J_{n-1} - J_{n+1} \\ 2n J_n & = J_{n+1} + J_{n-1},\end{split}\]

we can get two more useful relations,

\[\begin{split}\frac{d}{dz} (z^n J_n) & = z^n J_{n-1} \\ \frac{d}{dz} (z^{-n} J_{n}) & = - z^{-n} J_{n+1} .\end{split}\]

They are very useful when integrating by part.

Graphics and Properties

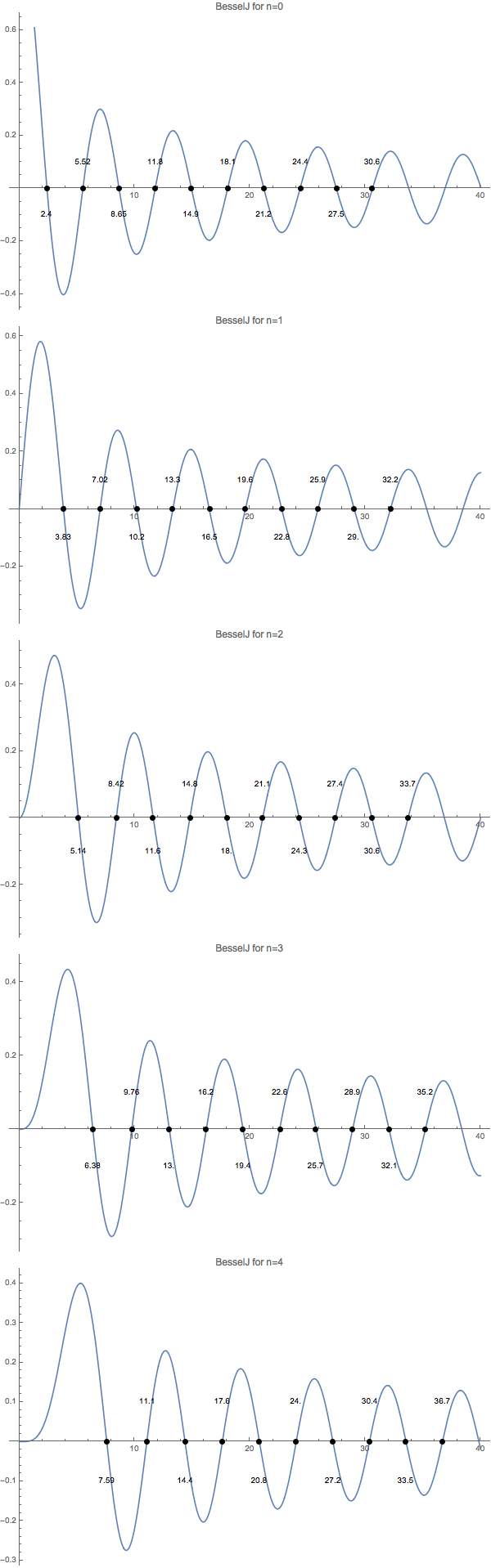
Fig. 4 The first 10 zeros of Bessel functions from order 0 to 4.

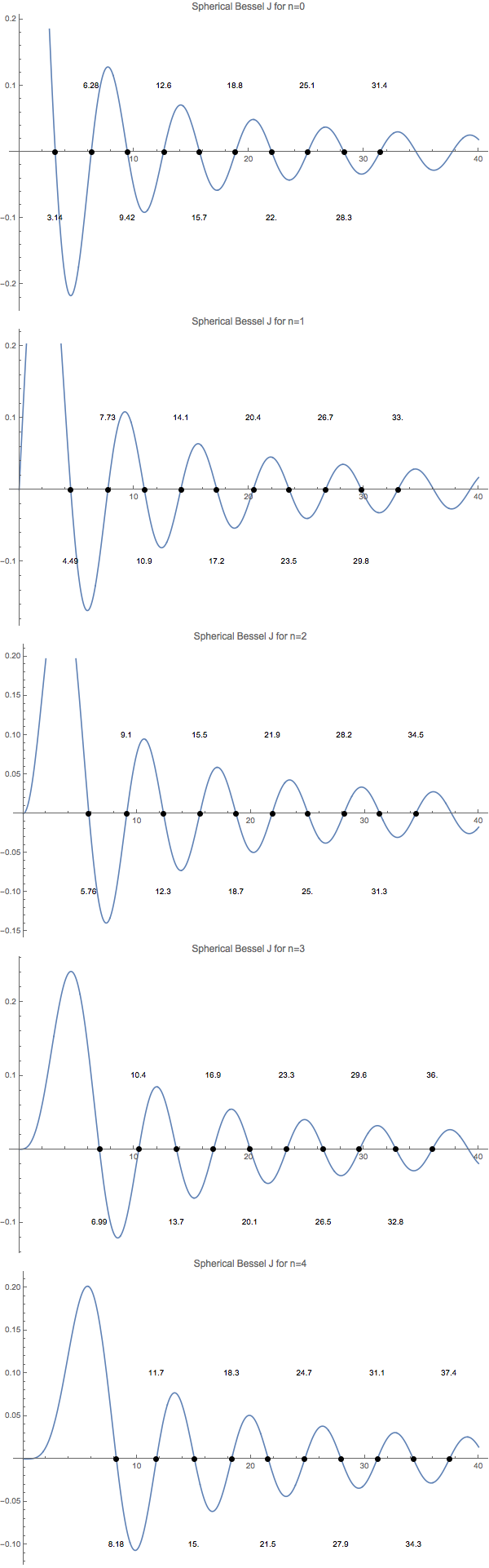
Fig. 5 The first 10 zeros of spherical Bessel functions from order 0 to 4.

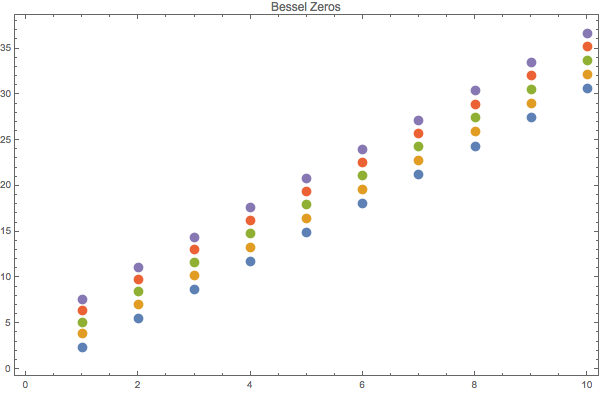
Fig. 6 Bessel function zeros in a list plot. Horizontal axis is nth zero point, while vertical axis is the value.

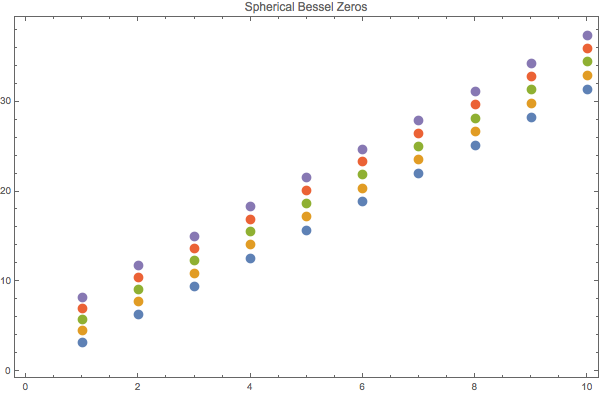
Fig. 7 Spherical Bessel function zeros.

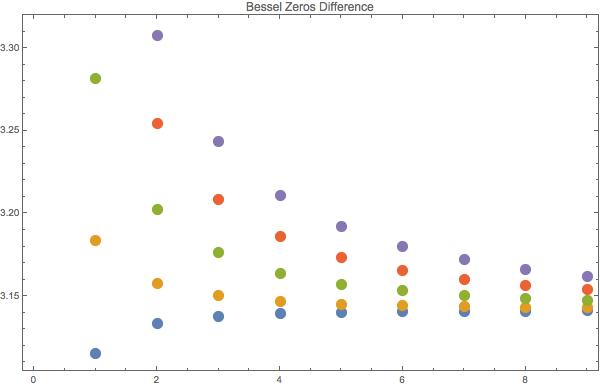
Fig. 8 The difference between zeros of Bessel functions. They are almost the same, which a around Pi.

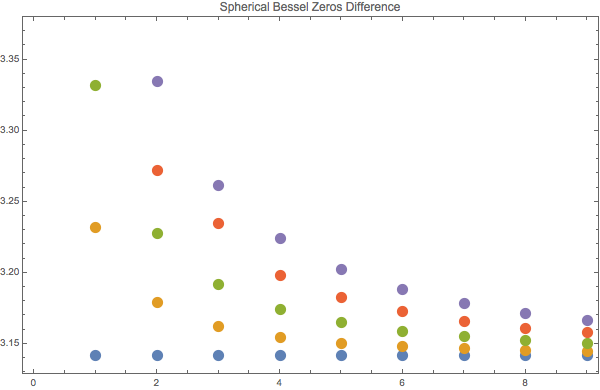
Fig. 9 Spherical Bessel function zeros differences.

Refs & Notes