Special Relativity¶

Notations

We use abstract index notation for most cases. A tensor with latin indices is an abstract tensor which tells us the rank of it but has no intention to indicate the components or basis.

We talk about transformations all the time in physics. For space and time, we also have the transformations from one reference frame to another, which plays the key role of our theories. Newtonian mechanics transform each space and time coordinates independently in translations. This idea was simply a extrapolation of our daily life experience that translations only change space coordinates accordingly, i.e.,

\[\begin{split}\begin{pmatrix} t'\\ x' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ -v & 1 \end{pmatrix}\begin{pmatrix} t\\ x \end{pmatrix}\end{split}\]

for the two reference systems described in Fig. 17. This transformation matrix is neither symmetric nor Hermitian. It is ugly and unexpected. Why is time special and is not related to other coordinates?

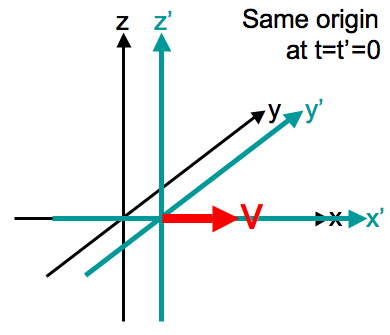
Fig. 17 Galilean transformation. Source: Wikipedia

As we think of this description, we would expect a most general transformation of coordinates for translation that involves all the coordinates, even for time.

\[\begin{split}\begin{pmatrix} t' \\ x'\\ y'\\ z' \end{pmatrix} = \begin{pmatrix} L_{11} & L_{12} & L_{13} & L_{14}\\ L_{21} & L_{22} & L_{23} & L_{24}\\ L_{31} & L_{32} & L_{33} & L_{34}\\ L_{41} & L_{42} & L_{43} & L_{44} \end{pmatrix}\begin{pmatrix} t \\ x\\ y\\ z \end{pmatrix}.\end{split}\]

How to determine this transformation matrix \(\mathbf L\)? Geometrically, we should conserve length since it’s a scalar, which is

(9)¶\[\eta^a_b x^a x^b,\]

where \(\eta_{ab}\) is the metric. More specifically,

\[\eta^a_b (L^a_cx^c )(L^b_d x^d ) = \eta^a_b x^a x^b.\]

In order to derive special relativity, we have to deterimin this metric \(\eta_{ab}\).

Physically or historically, we should preserve Maxwell’s equation, since it has been proved to be true in different reference frames.

What people found is that the geometry is hyperbolic geometry, hence the metric is Minkowskian.