Forms¶
Forms are used in many contexts of relativity. It might be difficult to visualize a general n-form, 1-form, on the other hand, carries a simple geometrical meaning even to physicists.
1-form can be viewed as the dual space of vectors. In many textbooks, vectors are named as contravariant vectors. In any case, vectors are visualized using arrows.
By definition, contraction of 1-form \(\tilde \omega\) and a vector \(v^a\) should result in a number. In the field of relativity, we talk about real fields, so
A 1-form maps a vector to a real number. From this point of view, 1-form is a set of contour lines. Given this set of contour lines, it maps an arrow to a number.
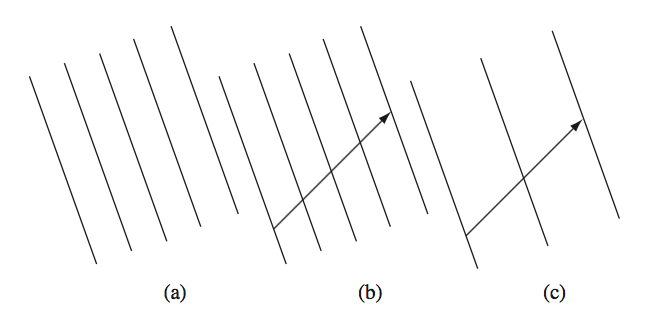
Fig. 16 1-forms as contour lines. Figure (a) shows a 1-form using contour lines in a neighbourhood of a point. Figure (b) shows how a 1-form (contour lines) maps a vector (arrow) to a real number. In this case, we could assign the result real number as the number of contour lines that the arrow crossed. Different 1-forms (contour lines) take the same vector (arrow) to different real number, 4 and 2 using our definition for (b) and (c). Taken from [Schutz].