Hyperbolic Geometry

Physics students are in fact quite familiar with the properties of hyperbolic geometry, even though some of the terms are not usually used in physics.

Visualizations of Hyperbolic Space

A lot of models are used to describe hyperbolic space

Numerious models are developed to describe the hyperbolic space.

1. Klein model;
2. Poincare model;
3. Gans model;
4. Weierstrass model or hyperboloid mode.

One of the useful visualizations of hyperbolic space is the the hyerboloid model, a.k.a. Weierstrass model. As the name indicates, hyperbolic space is embeded in Euclid space as a hyperboloid.

Hyperboloid on Two Sheets

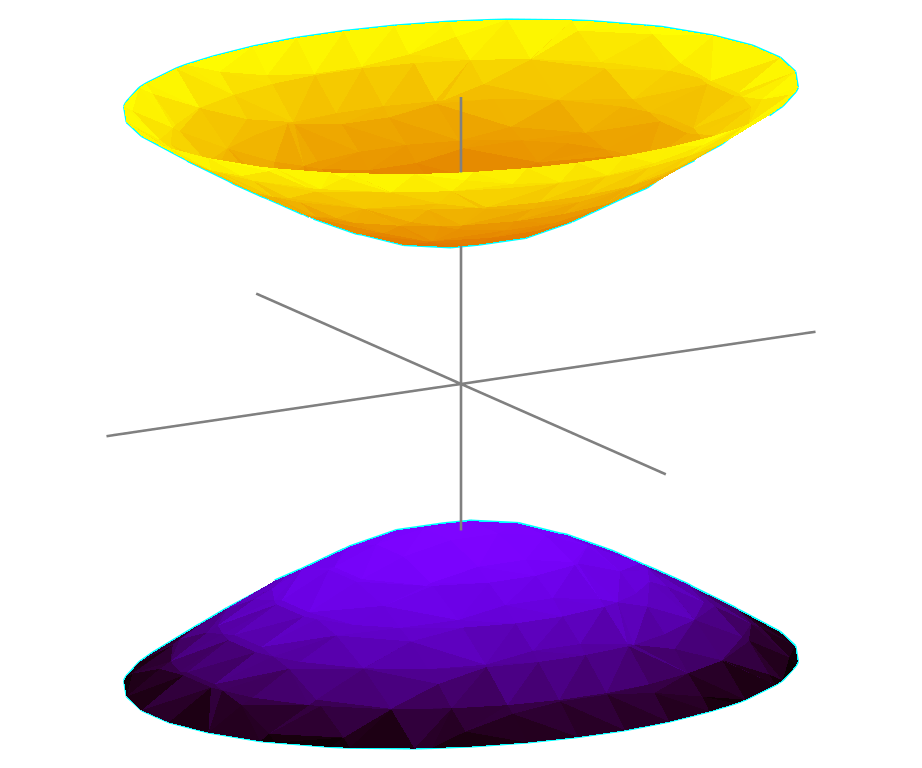
Fig. 18 Hyperboloid on two sheets. Source: Wikipedia.

A unit hyerboloid is described by the equation

\[x^2 + y^2 - z^2 = -1 ,\]

where \(x,y,z\) are the coordinates.

Lines on a hyperboloid is defined by the intersection of a plane with the hyperboloid.

We would also imagine that the so called light cone is basically

\[x^2 + y^2 - z^2 = 0.\]

For simplicity, we consider two dimensions, space \(x\) and time \(t\). To build a theory of special relativity, we have to first specify the distance on hyperbola geometry. It’s straightforward as it seems to be, we just extract distance from the definition of hyperbola since it is a conserved quantity,

\[\eta^\mu_\nu x^\mu x^\nu = x^2 - t^2.\]

For a standard hyperbola \(x^2-t^2=1\), we can parameterize the coordinates using a single parameter,

\[\begin{split}t =& \sinh\beta \\ x =& \cosh\beta,\end{split}\]

since

\[\cosh^2\beta - \sinh^2\beta = \Delta s^2.\]

Hyperbolic Trig Identities

As a review, the hyperbolic functions are defined as

\[\begin{split}\sinh\beta =& \frac{e^x - e^{-x}}{2}\\ \cosh\beta=& \frac{e^x + e^{-x}}{2}\\ \tanh\beta=& \frac{\sinh\beta}{\cosh\beta}\\ \coth\beta=& \frac{1}{\tanh\beta}\\ \csch \beta =& \frac{1}{\sinh\beta}\\ \sech \beta =& \frac{1}{\cosh\beta}.\end{split}\]

Hyperbolic trig functions have several identities that could help us with the understanding of the geometry.

\[\begin{split}\cosh^2 \beta - \sinh^2\beta =& 1 \\ \tanh^2\beta + \sech ^2 \beta =& 1\\ \coth ^2 \beta - \csch ^2 \beta=&1.\end{split}\]

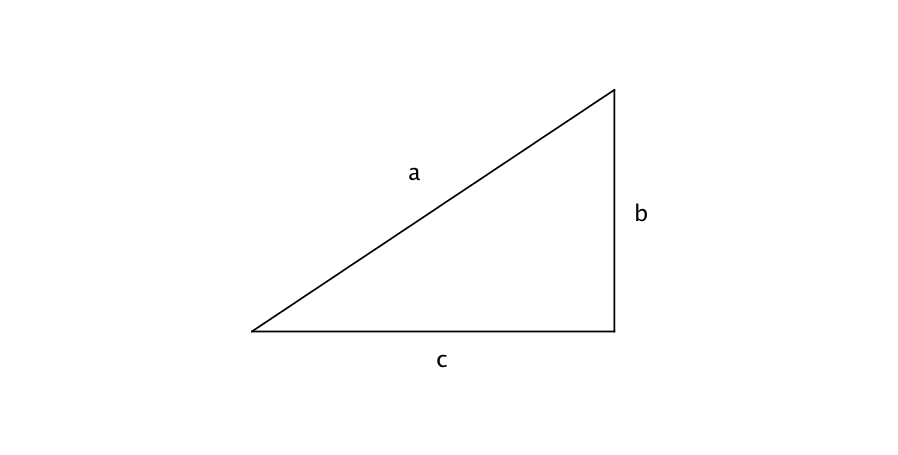
Fig. 19 Triangle of hyperbolic trig functions.

To visualize such relations, we draw an triangle, Fig. 19. We use this triangle to illustrate \(\sin\beta=b/a=3/4\)

We choose the edge \(b=3\) and \(a=4\). Given the condition that

\[\begin{split}\cosh\beta=&c/a\\ =&\sqrt{1+\sinh^2\beta}\\ =&\sqrt{1+3^2/4^2}=5/4,\end{split}\]

we have to set

\[c = 5,\]

which is not so intuitive from Fig. 19.