Doppler Effect

Doppler shift in special relativity is always confusing. I’ll demonstrate doppler shift in four different ways.

Conservation of Four Momentum

The special relativistic doppler shift can be derived using the fact that 4-momentum is a vector thus it transforms under Lorentz transformation.

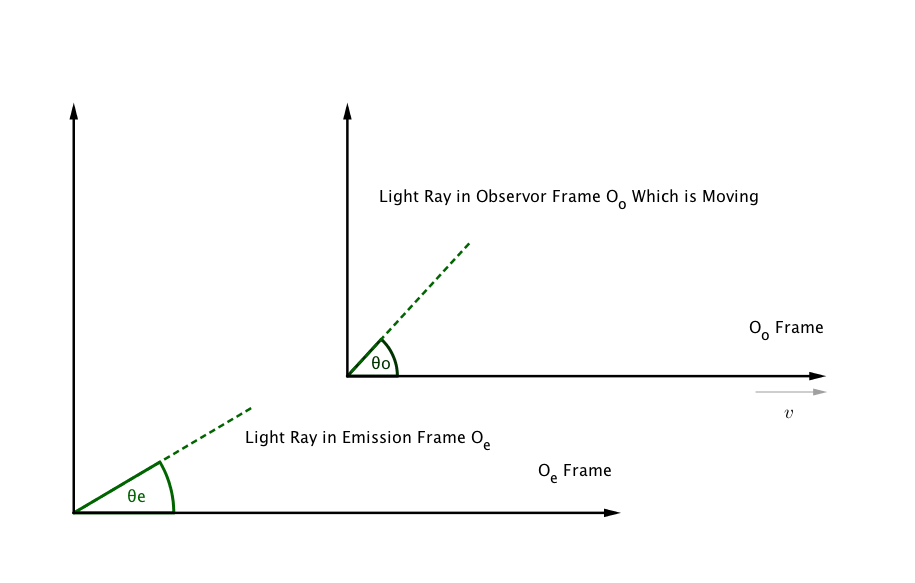
Fig. 21 The observer frame is moving in x direction only.

The observer is fixed in observer frame and source of emission is in emission frame.

The observer detects an angle of light ray \(\theta_o\). However, the emission angle \(\theta_e\) is different from this angle, i.e., \(\theta_e \neq \theta_0\).

Which Angle to Use

Which angle to use then? In theory, we can derive the Doppler shift in terms of either angles. We present both of the analysis. The redshift expressions looks different because they are measuring different events.

Components of four momentum in observer frame is

\[p_o^\mu = \begin{pmatrix} E_o & E_o \cos\theta_o & E_o\sin\theta_o & 0 \end{pmatrix}.\]

The components in the emission frame is

\[p_e^\mu = \begin{pmatrix} E_e & E_e \cos\theta_e & E_e\sin\theta_e & 0 \end{pmatrix}.\]

Redshift

Redshift is define as

\[\begin{split}z &= \frac{\nu_e - \nu_o}{\nu_o} \\ & = \frac{\omega_e - \omega_o}{\omega_o}.\end{split}\]

Non-relativistic Doppler Shift

To understand the effect of relativity, we would first recall the non-relativistic doppler shift.

(11)\[\omega_{o,non-rel} = \omega_{e,non-rel}(1-v/c \cos\theta).\]

where no \(\gamma\) is relavent. It’s obvious that we have only two kinds of shift, redshift due to the source is closing, or blueshift due to the fact that the source is moving away.

Redshift Relation to Angle in Emission Frame

Since momentum is a vector, we have the Lorentz transformation which transfrom it in to \(O_o\) frame,

\[\frac{E_o}{c} = \gamma \left(\frac{E_e}{c} - \beta p_e^1\right),\]

where we also have

\[\begin{split}p_e^1 &= p_e^0\cos\theta_e,\\ p_e^0 &= E_e/c.\end{split}\]

Combining these equations, the energy of the photons in \(O_e\) frame is

\[E_o = E_e \gamma (1 - \beta \cos\theta_e).\]

In quantum mechanics, energy is related to angular frequency,

\[E_{o/e} = \hbar \omega_{o/e}.\]

The angular frequency in O’ frame is

(12)\[\omega_o = \omega_e \gamma (1-\beta \cos\theta_e).\]

In fact, \(\beta=v\) if we choose \(c=1\).

Redshift Relation to Angle in Observor Frame

The problem is, we know that \(\theta_e\neq\theta_o\). In many cases, it’s more convinient to obtain the angle in observation frame \(\theta_o\).

In this case, we Lorentz transform the representation of four momentum in observer frame (\(p_o^\mu\)) to emission frame (\(p_e^\mu\)).

\[\frac{E_e}{c} = \gamma(\frac{E_o}{c}+\beta p_o^1),\]

where

\[\begin{split}p_o^1 &= p_o^0 \cos \theta_o \\ p_o^0 &= E_o/c.\end{split}\]

We solve the angular frequency for photons in observer’s frame

(13)\[\begin{split}\omega_o &= \frac{\omega_e}{\gamma(1+\beta \cos \theta_o)}\\ &= \omega_e\frac{\sqrt{1-\beta^2}}{(1+\beta \cos \theta_o)},\end{split}\]

where in the last step we applied

\[\gamma = 1/\sqrt{1-\beta^2}.\]

Eq. (13) seems to be very different from (12). The reason is that we are measuring different events, due to the difference between \(\theta_e\) and \(\theta_o\).

Eq. (13) is what usually used in discussion of relativistic Doppler effect.

Line-of-sight Direction Same as Relative Velocity Direction

\(\theta_o=\theta_e=0\) gives us the most used Doppler shift

(14)\[\omega_o=\omega_e\sqrt{ \frac{1-\beta}{1+\beta} }.\]

\(\beta=v\) if we choose \(c=1\).

Relativistic Effect

Nonrelativistic Doppler shift (11) contains only the effect of line-of-sight relocity.

Relativistic Doppler shift (13) we have new contributions from relative velocity, which is the transverse redshift due to the \(\gamma\) factor or the contraction of time.

If the motion is in line-of-sight, Eq. (14) is reduced to the nonrelativistic Doppler shift for slow velocity \(v\) as we take only first order of its Tayler series.

For motion that is not along the line-of-sight, angle difference becomes important, since we have to choose the equal time surface.

An gif from wikipedia shows this explicitly,

Fig. 22 Image Source: File:XYCoordinates.gif

The change in wavelength is given by

\[\frac{\lambda_{obs} }{ \lambda_{src} }= \sqrt{ \frac{1 - \beta}{1 + \beta} } .\]

Four Vector Language

Doppler shift can be solve using abstract four vectors without going into a coordinate system [CBLiang].

First of all we associate the emission frame and observation frame with its own four velocities, \(V^a\) and \(U^a\).

From the knowledge of special relativity, we know that

\[E_o/c = -p^a U_a\vert_{obs},\]

where \(U^a\) is the four velocity of observer, subscript \({}_{obs}\) indicates this is the measurement at observation point.

The photon energy in emission frame is

(15)\[E_e/c = - p^a V_a\vert_{em},\]

which is calculated at the point of emission. \(V^a\) is the four velocity of the emission frame.

Since inner product is independent of the physical point in special relativity, we can calculate the both energy at the same physical point.

We also know that

\[\gamma = -V^a U_a,\]

which associates the four velcoities

(16)\[U_a = \gamma V_a + \gamma u_a,\]

where \(\gamma u_a\) is the three velocity component viewed by \(V_a\).

The Instataneous Frame Decomposition

We always have to define our equal time surface first. Here we can see that \(\gamma u_a\) is indeed a decomposition onto our spatial surface.

Multiply on both sides of Eq. (16) by \(V^a\),

\[V^a u_a =0.\]

We also know from Eq. (15)

\[p^a = \omega V^a + k^a.\]

To collect our thoughts, we have obtained from the four momentum and our velocities \(u^a\) and \(k^a\), which are the quantities we would like to work on in 3D space.

Finally, we calculate the frequency in observer’s frame,

\[\begin{split}\omega_o &= -p^a U_a \\ &=-(\omega V^a + k^a)(\gamma V_a + \gamma u_a) \\ & = \gamma (\omega - k^a u_a),\end{split}\]

where

\[k^a u_a = v \omega \cos \theta_e.\]

Then we obtain the Doppler shift equation

\[\omega_o = \omega_e \gamma (1-v\cos\theta_e).\]

We can work out this using another projection of spatial dimensions, which is give us the frequency relation in terms of observation angle \(\theta_o\).

[CBLiang]

梁灿彬，周彬，《微分几何与广义相对论入门》

Spacetime Diagram

Needless to say, it can be explained using spacetime diagram. The only caveat is to pay attention to the equal time surface.

I am just too lazy to make a spacetime diagram with six axes here. You get the idea.